TAREA MATLAB

EJERCICIO 2.
EJERCICIO 4.
EJERCCIIO 5.
EJERCICIO 6.
EJERCICIO 7.
EJERCICIO 8.
EJERCICIO 13.
EJERCICIO 14.

%Tarea3_Matlab
clc; clear all; close all;

EJERCICIO 2.

Hallar el vector X para la siguiente ecuación matricial:

A=[4 -2 -10; 2 10 -12; -4 -6 16];
B=[-10; 32; -16];
X = B\A

X =

    0.0638    0.3159   -0.3913

EJERCICIO 4.

Hallar los autovalores y autovectores de la matriz A:

A=[0 1 -1; -6 -11 6; -6 -11 5];
[X,D]=eig(A);
AUTOVALORES=X
AUTOVECTORES=D

AUTOVALORES =

    0.7071   -0.2182   -0.0921
    0.0000   -0.4364   -0.5523
    0.7071   -0.8729   -0.8285


AUTOVECTORES =

   -1.0000         0         0
         0   -2.0000         0
         0         0   -3.0000

EJERCCIIO 5.

Para el siguiente circuito, determinar los voltajes de los nodos V1 y V2 y la potencia entregada por cada fuente:

R=[1.5-2.0i -0.35+1.2i; -0.35+1.2i 0.9-1.6i];
I=[30+40i; 20+15i];
V = I\R;
V1=V(1)
V2=V(2)
S1=V(1)*conj(I(1))
S2=V(2)*conj(I(2))

V1 =

  -0.0077 - 0.0290i


V2 =

   0.0101 + 0.0014i


S1 =

  -1.3920 - 0.5640i


S2 =

   0.2232 - 0.1224i

EJERCICIO 6.

Escribir una funcion recursiva para resolver el problema de la Torres de Hanoi y probarla para un valor 5 discos.

%n=input('Numero de discos en torre: ');
n=5;
fprintf('Llamando a la funci%cn Hanoi',243);
hanoi(n,'a','b','c');

Llamando a la función Hanoimover disco 1 de a a c
mover disco 2 de a a c
mover disco 1 de c a b
mover disco 3 de a a c
mover disco 1 de c a b
mover disco 2 de c a b
mover disco 1 de b a a
mover disco 4 de a a c
mover disco 1 de c a b
mover disco 2 de c a b
mover disco 1 de b a a
mover disco 3 de c a b
mover disco 1 de b a a
mover disco 2 de b a a
mover disco 1 de a a c
mover disco 5 de a a c
mover disco 1 de c a b
mover disco 2 de c a b
mover disco 1 de b a a
mover disco 3 de c a b
mover disco 1 de b a a
mover disco 2 de b a a
mover disco 1 de a a c
mover disco 4 de c a b
mover disco 1 de b a a
mover disco 2 de b a a
mover disco 1 de a a c
mover disco 3 de b a a
mover disco 1 de a a c
mover disco 2 de a a c
mover disco 1 de c a b

EJERCICIO 7.

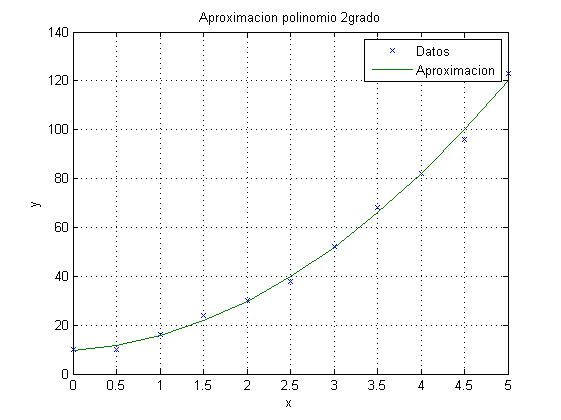
Ajustar un polinomio de orden 2 a los siguientes datos:

x=[0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0];
y=[10 10 16 24 30 38 52 68 82 96 123];
pol=polyfit(x,y,2);
fprintf('Polinomio: %ix^2 + %ix + %i\n',pol(1),pol(2),pol(3));
ye=polyval(pol,x);
plot(x,y,'x',x,ye);
xlabel('x')
ylabel('y')
grid on
title('Aproximacion polinomio 2grado')
legend('Datos','Aproximacion')

Polinomio: 4.023310e+00x^2 + 2.010723e+00x + 9.678322e+00

EJERCICIO 8.

Ajustar un polinomio de orden 2 a los siguientes datos:

figure
%1
    wt=0:0.05:3*pi;
    v1=120*sin(wt);
    i1=100*sin(wt -pi/4);
    subplot(2,2,1)
    plot(wt,v1,wt,i1)
%2
    p=v1.*i1;
    subplot(2,2,2)
    plot(wt,p)
%3
    Fm=3.0;
    fa=Fm*sin(wt);
    fb=Fm*sin(wt-2*pi/3);
    fc=Fm*sin(wt-4*pi/3);
    subplot(2,2,3)
    plot(wt,fa,wt,fb,wt,fc)
%4
    FR=3.0
    x=cos(wt);
    y=sin(wt);
    subplot(2,2,4)
    plot(FR*x,FR*y)

FR =

     3

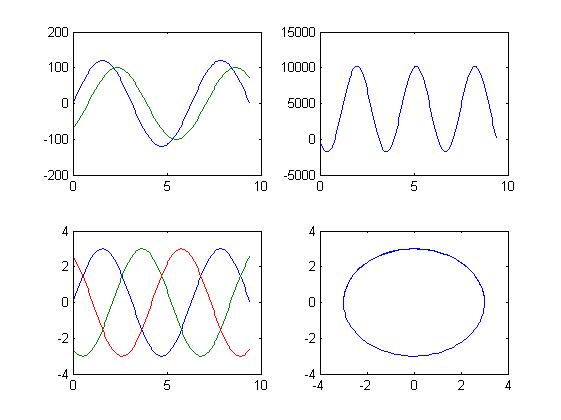
EJERCICIO 13.

Tomando como base las condiciones del ejemplo de la transformada de Fourier de los apuntes (pág. 124), graficar para las siguientes señales la grafica de la señal en el tiempo y la grafica de la amplitud espectral en funcion de la frecuencia:

k = 5;   m = 10;   fo = 10;   Bo = 2.5;
N = 2^m;   T = 2^k/fo;
ts = (0:N-1)*T/N;
df = (0:N/2-1)/T;
%1
SampledSignal1 = Bo*sin(2*pi*fo*ts)+Bo/2*sin(2*pi*2*fo*ts);
An = abs(fft(SampledSignal1, N))/N;
figure
subplot(1,2,1)
plot(ts, SampledSignal1)
subplot(1,2,2)
plot(df, 2*An(1:N/2))
%2
SampledSignal2 = exp(-2*ts).*sin(2*pi*fo*ts);
An1 = abs(fft(SampledSignal2, N))/N;
figure
subplot(1,2,1)
plot(ts, SampledSignal2)
subplot(1,2,2)
plot(df, 2*An(1:N/2))
%3
SampledSignal3 = sin(2*pi*fo*ts + 5*sin(2*pi*fo/10*ts));
An2 = abs(fft(SampledSignal3, N))/N;
figure
subplot(1,2,1)
plot(ts, SampledSignal3)
subplot(1,2,2)
plot(df, 2*An(1:N/2))
%4
SampledSignal4 = sin(2*pi*fo*ts - 5*exp(-2*ts));
An3 = abs(fft(SampledSignal4, N))/N;
figure
subplot(1,2,1)
plot(ts, SampledSignal4)
subplot(1,2,2)
plot(df, 2*An(1:N/2))

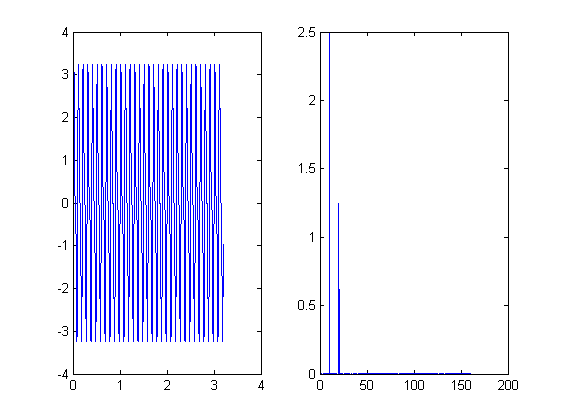
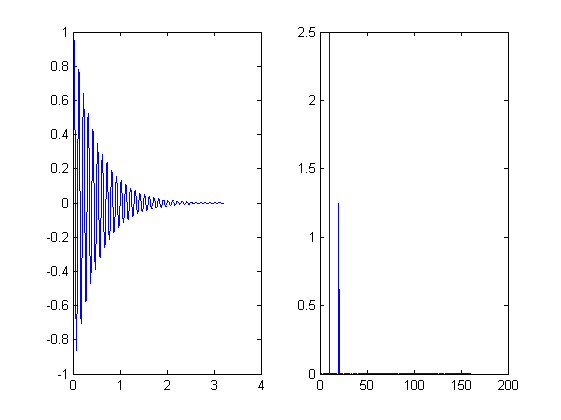
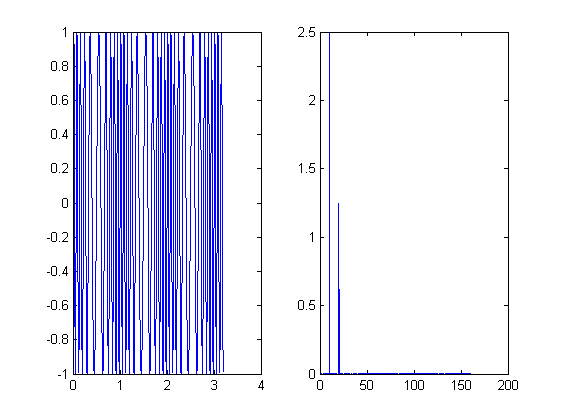
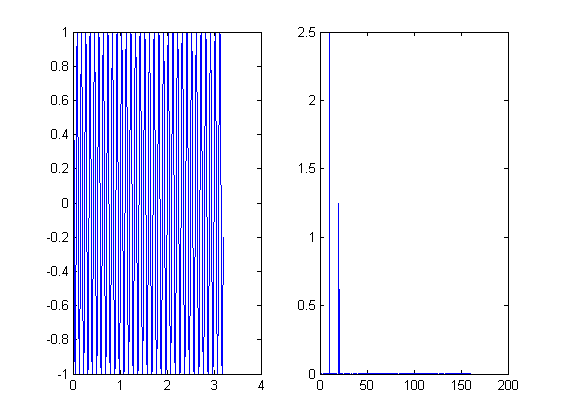
EJERCICIO 14.

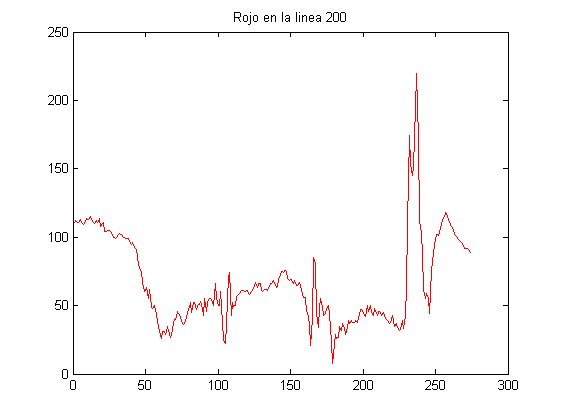
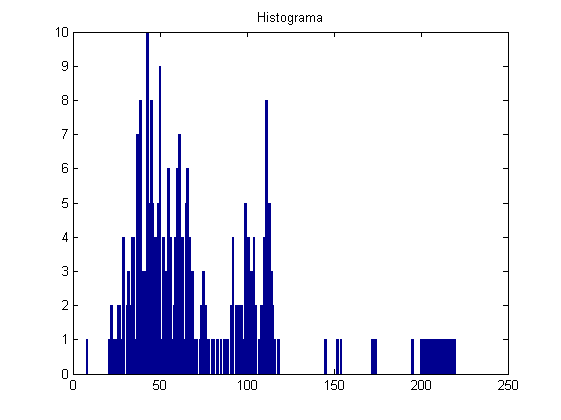
Leer y graficar la imagen WindTunnel.jpg de las transparencias y graficar en sendos graficos el valor del color rojo de la imagen en función del ancho de la imagen y el histograma del mismo para una fila de la imagen que se pide al usuario. Mostrar el valor para 200

figure
A = imread('WindTunnel.jpg', 'jpeg');
image(A)
figure
row = 200;
red = A(row, :, 1);
plot(red, 'r');
title('Rojo en la linea 200');
figure
hist(red,0:1:200);
title('Histograma' );

Contents